VU | Metody statystyczne (ćwiczenia) - <b style="color:#05ffac">studia niestacjonarne</b>

Organizacja
Zestaw 1
- Generator liczb losowych
- Ruina gracza
Zestaw 2
- Symulacja procesu Markova
- Process Poissona
Zestaw 3
- Symulacja procesu kolejkowego
Zestaw 4

Organizacja

Zajęcia będą prowadzone w sale G-1-03 (lub z wykorzystaniem MS TEAMS - pod czas zjazdów zdalnych). Na każdym spotkaniu studenci otrzymają zestaw zadań (będzie on udostępniany na tej stronie).

Zadania zaliczane są podczas trwania zajęć, wystarczy zademonstrować działanie odpowiedniego programu oraz krótko o nim opowiedzieć. Za każde zaliczone zadanie student dostaje 1 punkt. Studenci mają również możliwość dorobić zadania w domu, ale ono muszą być oddane nie później niż na kolejnych zajęciach. Za każde zadanie oddane po ukończeniu odpowiednego terminu, studenci dostają 0.5 punkta. Do wykonania zadania każdy może wybrać dowolny język lub środowisko programistyczne, jednak zabronione jest używanie jakichkolwiek bibliotek i funkcji statystycznych lub pomocniczych.

Minimalnym warunkiem zaliczenia jest dostanie 2 punktów z każdego zestawu. Jednak liczba punktów wpłynie na ocenę końcową, więc im więcej zadań zastanie wykonane, tym lepiej. Konkretna skala ocen będzie podana przed końcem semestru.

Zestaw 1

26.11.2022

Grupa 2: 08:00 - 10:15
Grupa 1: 10:30 - 12:45

Slajdy

Generator liczb losowych

Problem A1
1. Implementacja generatora liczb losowych z rozkładu normalnego $N(0,1)$ metodą polarną
2. Narysowanie histogramu i porównanie ze wzorem analitycznym
3. Obliczyć eksperymentalne wartości średniej oraz wariancji
Problem A2
1. Implementacja generatora liczb losowych z rozkładu Cauchy’ego $C(y_0,\gamma)$, metodą odwróconej dystrybuanty: $\begin{equation} f(y) = \frac{1}{\pi\gamma\left[1+\left(\frac{y-y_0}{\gamma}\right)^2\right]}, \qquad y \in (-\infty, \infty)\nonumber \end{equation}$
2. Narysowanie histogramu i porównanie ze wzorem analitycznym dla różnych wartości $y_0$ i $\gamma$
3. Obliczyć eksperymentalne wartości średniej oraz wariancji

Ruina gracza

Ruina gracza dla 2 graczy: gracz A z kapitałem początkowym a i gracz B z kapitałem początkowym b. Po każdej rozgrywce wygrywający gracz otrzymuje jedną jednostkę kapitału od przegranego. Nie ma remisów. $p_A$ - prawdopodobieństwo wygranej gracza A w jednej rozgrywce (dla dwóch graczy $p_B = 1- p_A$).

Dla każdego z problemów wyniki są pobierane z zaimplementowanej symulacji gry(gier) ruiny gracza.
N - parametr który wyznaćza ilość symulowanych gier, dla różnych zadań ten parametr może być różnym (generalnie im więcej tym lepiej, może być wybrany tak, żeby symulacją nie trwała za długo).

Problem B
a = 50, b = 50
Symulacja N gier z różnymi wartościami $p_A$. Dla każdej wartości obliczyć prawdopodobieństwo ruiny gracza A.
1. Wykres $P_{ruiny}(p_A)$ - zależności prawdopodobieństwa ruiny gracza A od prawdopodobieństwa wygranej w jednej rozgrywce $p_A$
2. Porównanie z wynikiem teoretycznym
3. Spróbować dla różnych wartości a i b
Problem C
a + b = 100;
$p_A = \frac{1}{2}$
Symulacja N gier z różnymi wartościami a. Dla każdej wartości obliczyć prawdopodobieństwo ruiny gracza A.
1. Wykres $P_{ruiny}(a)$ - zależności prawdopodobieństwa ruiny gracza A od początkowego kapitału a
2. Porównanie z wynikiem teoretycznym
3. Spróbować dla różnych wartości $p_A$
Problem D
L - liczba rozgrywek do ukończenia gry
$p_A = \frac{1}{2}, \frac{1}{5}, \frac{4}{5}$;
a = b=50
Proponowana całkowita liczba gier N = 20000
Symulacja N gier, dla każdej gry obliczyć ilość rozgrywek.
1. Histogram prawdopodobieństwa P(L) - liczby rozgrywek do ukończenia gry
2. Wyliczyć średnią długość rozgrywki
Problem E
N - wybrana wartość symulowanych gier
Symulacja N gier z różnymi wartościami $p_A$. Dla każdej wartości $p_A$ obliczyć maksymalną ilość rozgrywek.
1. Wykres $L_{max}(p_A)$ - maksymalna długość rozgrywek $L_{max}$ przy N rozgrywkach jako zależność od wartości $p_A$
Problem F
n = 2,10,20,…,100
a = b = 50
$p_A = \frac{1}{2}, \frac{1}{5}, \frac{4}{5}$
Symulacja n rozgrywek N razy.
1. Histogram prawdopodobieństwa P(M) - że gracz A ma kapitał M po n rozgrywkach
Problem G
Symulacja kilku gier (do 10)
spróbować dla różnych wartości $p_A$
1. Wykres trajektorii liczby wygranych jednego z graczy jako zależność od numera rozgrywki
2. Wykres trajektorii kapitału jednego z graczy jako zależność od numera rozgrywki
Problem H
Problemy B, C, D, G dla kilku, np. pięciu, graczy.
Różne kombinacje wartości $p_i$ - prawdopodobieństw wygranej dla gracza numer $i$.
$a_i$ = 20 - kapitały początkowe gracze (lub spróbować inne wartości). (jeden punkt za każdy problem)

Zestaw 2

11.12.2022

Grupa 2: 08:00 - 10:15
Grupa 1: 10:30 - 12:45

Slajdy

Symulacja procesu Markova

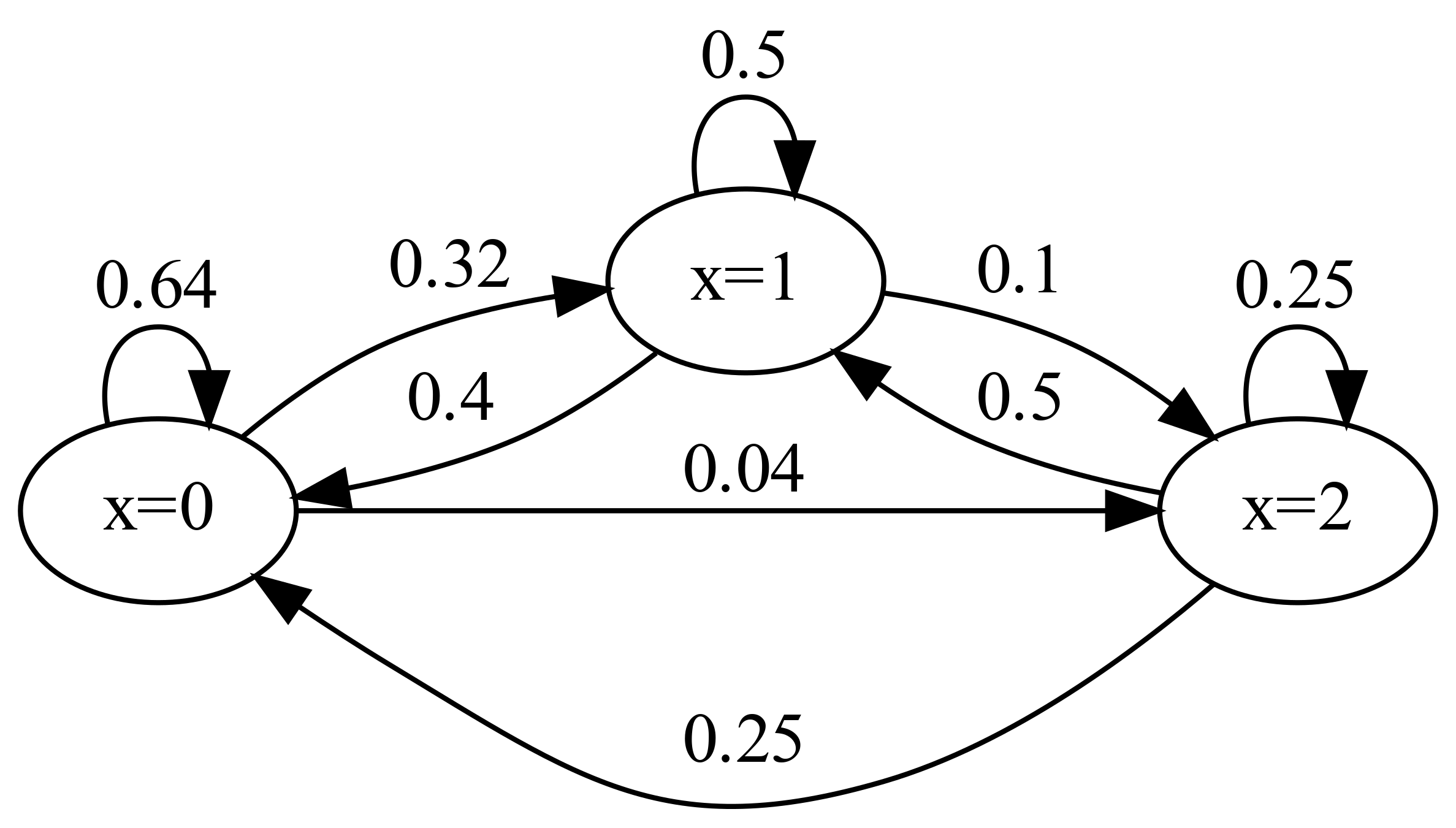
Mamy 2 użytkownika i każdy z nich może być zalogowanym lub niezalogowany do komputera, niezależnie od drugiego. Prawdopodobieństwo zalogowania dla użytkownika jest $P_{zalogowania} = 0.2$, wylogowania - $P_{wylogowania} = 0.5$. W takim przypadku mamy trzy możliwych stany: zalogowanę są 0, 1 lub 2 użytkowniki. Na diagramie powyżej x - ilość zalogowanych użytkowników i strzałki określają przejście z jednego stanu do innego z odpowiednim prawdopodobieństwem. W danym przypadku macierz przejść:

\[\begin{equation*} P = \begin{pmatrix} 0.64 & 0.32 & 0.04\\ 0.4 & 0.5 & 0.1 \\ 0.25 & 0.5 & 0.25 \end{pmatrix} \end{equation*}\]

Problem A
1. Policzyć $P^N$ dla dużych N
2. Kryterium zbieżności: $\mid P^n - P^{n-1}\mid < \epsilon$
3. $\epsilon = 10^{-5}$ lub inne wartości
4. Narysować wykres $[P^n]_{ij}$ w zależności od n
5. Porównanie z wartościami $\pi_j$ na wykresie
Problem B
1. Symulacja procesu Markova
  - Zaczynamy z wybranego węzła $x = \{0,1, 2\}$
  - Losowanie kolejnego węzła zgonie z $P$
  - Przejście do losowanego węzła
  - Powtarzamy
2. Losujemy $N=10^4$ przejść
3. Obliczenie $\pi_i^{exp} = \frac{N_i}{N}$,
  $N_i$ - ile razy odwiędzone $x=i\quad(0,1,2)$
4. Porównanie z $P^N$
5. Start z różnych węzłów
Problem C
100 użytkowników → trudno jest obliczyć macierz prawdopodobieństw
$x=0,1,2,...,100$;
$P_{logowania} = 0.2$, $P_{wylogowania} = 0.5$
1. Wykonujemy symulację trajektorii (zaczynamy z dowolnego węzła $x$)
2. Ile wynosi $\pi^{exp}_i$ dla $i=0,1,\cdots,100$?
3. Wykresy zbieżności $\pi^{exp}_i = \frac{N_i}{N}$ jako zależność od $N$ dla kilku $i$ (np dla pięciu największych wartości $\pi$)
4. Wykres końcowych wartości dla wszystkich $\pi^{exp}_i$
Problem D
Podobna symulacja jak w C, tylko
1. $P_{logowania} = 0.2$;
2. $P_{wylogowania} = 1 - (0.008 \cdot x+0.1)$ - dla węzła $x$;

Process Poissona

$t_i$ - czas pomiędzy zdarzeniami $(i-1)$ i $(i)$,
$i = 1,2,...$, $\qquad t_0=0$
$t_i$ jest losowane z rozkładu wykładniczego, $f(t) = \lambda e^{-\lambda t}$

losujemy $t_i$ metodą odwróconej dystrybuanty
$t_i = \frac{- \ln (n_i)}{\lambda}$;
$n_i$ losowane z rozkładu jednorodnego na przedziale (0,1)

$N(t)$ - ilość zdarzeń, które wystąpiły do chwili $t$, $N(0)=0$
Taki proces nazywa się procesem Poissona o intensywności $\lambda$
$N(t)$ ma rozkład Poissona $P (N(t)=k) = \frac{(\lambda t)^k}{k!}e^{-\lambda t}$, z parametrem $\lambda \cdot t$

Problem E
Symulacja procesu Poissona $\lambda = 1$
$t = 1,10,20,90$
1. Zaimplementować symulację pojawienia zdarzeń
2. Dla każdej wartości t:
  - otrzymać rozkład prawdopodobieństwa ilości zdarzeń
  - porównać z rozkłądem Poissona z parametrem $\lambda \cdot t$
  - sprawdzić że wartość średnia jest $\lambda \cdot t$
Problem F
Mamy symulację zdarzeń jak w E
$\lambda = 1$; $t = 1,10,20,90$
Każde zdarzenie może należeć do jednej z trzech grup: 1,2,3
Należność do jednej z grup jest losowane i prawdopodobieństwa należności do grup: $p_1 = 0.2$, $p_2 = 0.5$, $p_3 = 0.3$ ($p_1+p_2+p_3=1$)
1. Sprawdzić że rozkład prawdopodobieństwa zdarzeń grupy $i$ jest rozkładem Poissona z parametrem $\lambda \cdot t \cdot p_i$
2. Sprawdzić że wartość średnia dla takiego rozkładu jest $\lambda \cdot t \cdot p_i$

Zestaw 3

17.12.2022

zjazd zdalny

Grupa 2: 11:00 - 13:15
Grupa 1: 13:30 - 15:45

Slajdy

Symulacja procesu kolejkowego

Zaimplementowanie symulacji procesu kolejkowego z jednym serwerem.

Problem A
Symulacja procesu kolejkowego dla 10 zadań dla $\lambda_A = 2$, $\lambda_D = 2.5$.
Zrobić wykresy:
1. Liczba zadań w kolejce w zależności od czasu.
2. Czas oczekiwania na wykonanie w zależności od czasu.
3. Liczba wykonanych w zależności od czasu.
4. Powtórzyć dla $\lambda_A = 2$, $\lambda_D = 1.5$
Problem B
1. Sprawdzić prawo Little’a: $E(R) \lambda_A = E(n)$
  E(R) - średni czas spędzony przez zadanie w systemie ($R_i = D_i - A_i$)
  E(n) - średnia ilość zadań w kolejcę
2. $\lambda_A = 2$, $\lambda_D = 3$
3. Symulacja dla 1000 zadań
4. Sprawdzić również dla $\lambda_A = 2$, $\lambda_D = 5$
Problem C
1. Zaobserwować zatykanie systemu
2. $\lambda_A = 15$, $\lambda_D = 8$
3. n=1000 zadań
4. Wykresy jak w A
5. Pomyśleć co mogą znaczyć następne wzory (narysować wykresy i porównać z tymi które juz mamy) :
  $\begin{eqnarray*} (\lambda_A - \lambda_D)t\\ \frac{\lambda_A - \lambda_D}{\lambda_D}t \end{eqnarray*}$
Problem D
Zrobić następne wykresy:
1. E(liczba zadań) w zależności od $\lambda_A$
2. E(liczba zadań) w zależności od $\lambda_D$
3. E(liczba zadań) w zależności od $r = \frac{\lambda_A}{\lambda_D}$
4. … to samo dla E(czas oczekiwania)
E(x) - znaczy wartość oczekiwana
Problem E
Zrobić graf jak w poprzednim zestawie ale dla 3 użytkowników (dowolną metodą)

Zestaw 4

14.01.2023

Grupa 2: 10:30 - 12:45
Grupa 1: 13:00 - 15:15

Symulacja określania liczebności populacji metodą kolejnych złowień

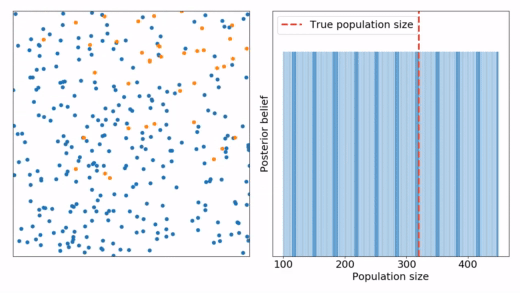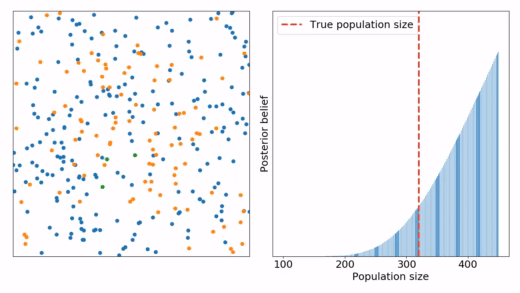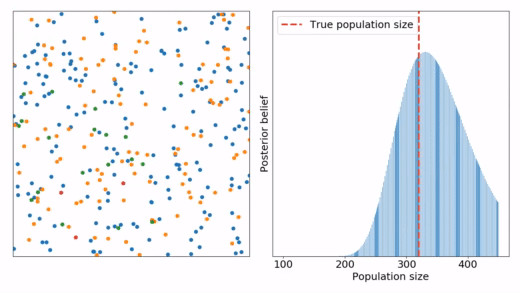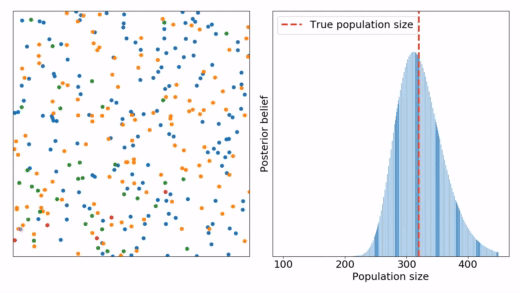
Mamy populacje rozmiaru N z której przez serie pomiarów łowimy pewną ilość osobników, oznakujemy ich i uwalniamy. Znając całkowitą ilość oznakowanych osób i porównując ją z liczbą ponownie złowionych - można oszacować rozmiar populacji.

Używamy dla tego Twierdzenie Bayesa, czyli prawdopodobieństwo tego że rozmiar populacji jest równy do $N_j$:

\[P(N_j|m, t, M) \propto \frac{P(m|N_j, t, M) P(N_j)}{\sum_i P(m|N_i, t, M) P(N_i)},\]

gdzie N_j - rozmiar populacji, M - całkowitą ilość oznakowanych osób, t - ilość złowionych osób w danym pomiarze, m - ilość ponownie złowionych w danym pomiarze.

$P(N_j)$ - prior - rokład prawdopodobieństwa przed pomiarem. Przed pierwszym pomiarem zakładamy że wierzymy w to że rozmiar populacji jest wartość losowa w pewnym przedziale $[a, b]$ i każda wartość z tego przedziału ma to samo prawdopodobieństwo. Czyli $P(N)$ jest z rozkładu jednorodnego i $P(N_j) = \frac{1}{b-a}$, dla wszystkich $N_j \in [a, b]$. W kolejnych pomiarach bierzemy $P(N)$ zako posterior z poprzedniego pomiaru.
$P(m\mid N_j, t, M)$ - likelihood - prawdopodobieństwo ponownie złowić m osób jeżeli rozmiar populacji jest N.
$P(N_j \mid m, t, M)$ - posterior - szukany rozkład prawdopodobieństwa że rozmiar populacji jest N.
$\sum_i P(m \mid N_i, t, M) P(N_i)$ - używany dla normalizacji.

Wartość $P(m \mid N_j, t, M)$ jest z rozkładu hipergeometrycznego:

\[P(m|N_j, t, M) = \frac{\binom{M}{m}\binom{N_j-M}{t-m}}{\binom{N_j}{t}},\]

gdzie Symbol Newtona:
$\binom{n}{k} \equiv \frac{n!}{k!(n-k)!}$

Zakładamy że rozmiar populacji jest stały i każda osoba ma takie same prawdopodobieństwo zostać złowioną.

Problem A
Sprawdzić że jeżeli przy kolejnym pomiarze złowiliśmy t osobników, to liczba ponownie złowionych osobników m jest zmienna z rozkładu hipergeometrycznego. Zakładamy że znamy wartości N (rozmiar populacji) i M (liczba złowionych poprzednio osób).
1. Zasymulować łosowanie t osobników z N populacji. Wielokrotnie powtarzając takie losowanie (wartość M jest stała, czyli złowione osoby nie dodajemy do listy), dostać rozkład prawdopodobieństwa dla wartości m.
  N = 50, M = 20, t = 12
2. Narysować histogram wygenerowanego rozkładu i porównać z teoretycznym.
Problem B
1. Zrobić symulację procesu metody kolejnych złowień.
2. N = 1000.
3. Zakładamy że rozmiar populacji jest w przedziale [0, 2000].
4. Liczba złowionych osób t dla każdego pomiaru jest losowana z rozkładu jednorodnego na przedziale $[40, 60]$.
5. Zrobić symulację 10 pomiarów.
6. Narysować wykres rozkładu prawdopodobieństwa rozmiaru populacji po każdym pomiarze.
Problem C
1. Dla wyników z Problemu B zrobić jeszce 10 pomiarów.
2. Po każdym pomiarze oszacować rozmiar populacji dwoma metodami:
  1. Znaleźć rozmiar który ma maksymalną wartość prawdopodobieństwa;
  2. Obliczyć wartość oczekiwaną: $(\bar{X}) = \sum_i P(X_i)*X_i$
3. Narysować wykres oszacowanych wartości w zależności od numeru pomiaru.
4. Narysować takie same wykresy ale na osi poziomowej będzie wartość M (całkowitą ilość oznakowanych osób w danym pomiarze).

21.01.2023

Grupa 2: 10:30 - 12:45
Grupa 1: 14:00 - 16:15

Oddanie zadań

4.02.2023

Grupa 2: 12:00 - 14:15
Grupa 1: 14:30 - 16:45

Kolokwium
Konsultacja / oddanie zadań